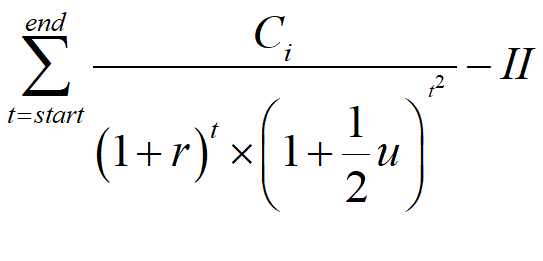Your Margin and Your Life
Chapter 12 from my forthcoming book Rebuilding Economics from the Top Down
Even I was shocked when I first plotted the data in Figure 56. While the private debt to GDP ratio grew by roughly 40% over the decade of the 1920s, the margin debt component of private debt grew far more quickly, from 1% of GDP in 1918 to 8.5% in 1929. Then it crashed, even more rapidly than it had risen, collapsing to half a percent of GDP in 1931. From then it was quiescent for decades, until a blip during the 1987 stock market bubble and crash, followed by its dramatic rise in the days of the "Greenspan Put",74F to which the '87 Crash gave birth.
This is Chapter 12 from my forthcoming book Rebuilding Economics from the Top Down, which will be published by the Budapest Centre for Long-Term Sustainability and the Pallas Athéné Domus Meriti Foundation. I am serialising the book chapters here. A watermarked PDF of the manuscript is available to supporters.
One look at this chart should be sufficient to understand why the Great Crash of 1929 was both great, and a major cause of the Great Depression which followed it, and why levered speculation, rather than rational calculation, dominates the behaviour of asset markets.
Figure 56: The margin debt that fuelled the speculative mania of the 1920s—and the 2000s
Free subscribers: if Substack’s $5/month is too much, consider supporting me via Patreon for $1/month or $10/year discounted
With margin loans enabling a borrower to purchase $100,000 worth of shares with only a $10,000 deposit, the 30% fall in the market over the month of October 29th, 1929, by itself wiped out the equity of many speculators. Those that were not taken out in that immediate crisis were largely accounted for in the subsequent fall of the Dow Jones Industrial Index (DJIA) from its peak of 381 in September 1929 to its nadir of 41 in July 1932—a fall of almost 90% that more than wiped out all the gains of the "Roaring Twenties" (see Figure 57).
Figure 57: The 1920s Stock Market Bubble and its aftermath
It should be obvious then, that a debt-based theory of asset pricing is needed. But au contraire, mainstream finance theory, in what is known as the "Modigliani-Miller Hypothesis" (Modigliani and Miller 1958), asserts that the increase in personal gearing shown in Figure 56 should have no effect on the value of shares, since the higher leverage of share buyers can be offset by lower leverage of companies themselves:
We conclude therefore that levered companies cannot command a premium over unlevered companies because investors have the opportunity of putting the equivalent leverage into their portfolio directly by borrowing on personal account. (Modigliani and Miller 1958, p. 273)
What became known as the "Capital Asset Pricing Model" or CAPM, after Sharpe's 1964 paper "Capital Asset Prices: A Theory of Market Equilibrium under Conditions of Risk" (Sharpe 1964), argued that a company's share price should simply reflect the rationally anticipated net present value of the income stream from the assets owned by the company. Except for the effect of laws enabling tax deductions for interest payments, share prices should be independent of leverage, whether of the companies themselves or their shareholders.
This proposition is strongly contradicted by the data. Figure 58 plots margin debt data against Robert Shiller's CAPE ("Cyclically Adjusted Price to Earnings" ratio) index (Bunn and Shiller 2014), and illustrates that share market valuation closely mirrors margin debt. Far from being zero, over the period 1926-2019, the correlation coefficient of margin debt to the CAPE is 0.56, while the correlation of change in margin debt and change in the CAPE is 0.74.
Figure 58: Share market valuation closely mirrors margin debt
Sharpe's theory, which is still taught today as the foundation of finance theory, must therefore be false—and it Is not hard to see why.
As is typical of Neoclassical reasoning, Sharpe first derived a theory of levered investing for a single individual, and then faced the dilemma of how to go from the isolated individual to the aggregate economy. As is also typical, his solution was to simply extrapolate from the individual to the aggregate:
In order to derive conditions for equilibrium in the capital market we invoke two assumptions. First, we assume a common pure rate of interest, with all investors able to borrow or lend funds on equal terms. Second, we assume homogeneity of investor expectations: investor are assumed to agree on the prospects of various investments-the expected values, standard deviations and correlation coefficients. (Sharpe 1964, pp. 433-34. Emphasis added)
Sharpe continued with a half-hearted defence of these manifestly false assumptions, using a distorted rendition of Friedman's methodological claim that a theory cannot be tested by its assumptions (Friedman 1953):
Needless to say, these are highly restrictive and undoubtedly unrealistic assumptions. However, since the proper test of a theory is not the realism of its assumptions but the acceptability of its implications, and since these assumptions imply equilibrium conditions which form a major part of classical financial doctrine, it is far from clear that this formulation should be rejected—especially in view of the dearth of alternative models leading to similar results. (Sharpe 1964, p. 434. Emphasis added)
He later elaborated upon the falsity and fragility of these assumptions:
By assumption, there is complete agreement about future prospects. Even the most casual empiricism suggests that this is not the case. People often hold passionately to beliefs that are far from universal. The seller of a share of I BM stock may be convinced that it is worth considerably less than the sales price. The buyer may be convinced that it is worth considerably more… (Sharpe 1970, p. 104)
Sharpe ultimately concluded that:
The consequences of accommodating such aspects of reality are Iikely to be disastrous in terms of the usefulness of the resulting theory…
The capital market line no longer exists Instead there is a capital market curve—linear over some ranges, perhaps, but becoming flatter as p increases over other ranges. Moreover, there is no single optimal combination of risky securities; the preferred combination depends on the investors' preferences. In short, the separation theorem no longer holds.
The demise of the capital market line is followed immediately by that of the security market line. The theory is in a shambles. (Sharpe 1970, p. 111-12. Emphasis added)
Despite this concession to reality, Sharpe clung to his model for much the same reason that Blanchard clung to micro-based macroeconomics: because he could not conceive of an alternative. He also asserted that "It is the essential theory for positive applications" because "it yields implications sufficiently strong to be tested empirically" (Sharpe 1970, p. 113).
By 2004, the results of those empirical tests were in—and they strongly contradicted the CAPM. Given the still-prevalent teaching of the CAPM model by university economics and finance departments, the paper "The Capital Asset Pricing Model: Theory and Evidence" by two one-time champions of the model, Fama and French, deserves to be widely read.
They conclude that "the empirical record of the model is poor—poor enough to invalidate the way it is used in applications" (Fama and French 2004, p. 25). Its fantastical assumptions, which were approved by Neoclassical economic referees at its inception, were singled out by Fama and French in 2004 as the primary reasons why it was an empirical failure. These were not only the common risk-free interest rate and "homogeneity of investor expectations" admitted to by Sharpe, but further that these expectations were correct—or in other words, CAPM is based on the assumption that investors can accurately predict the future. Though their expression of this condition is obtuse, that is what the words highlighted below mean:
Sharpe (1964) and Lintner (1965) add two key assumptions to the Markowitz model to identify a portfolio that must be mean-variance-efficient. The first assumption is complete agreement given market clearing asset prices at , investors agree on the joint distribution of asset returns from to . And this distribution is the true one—that is, it is the distribution from which the returns we use to test the model are drawn. (Fama and French 2004, p. 26. Boldface emphasis added)
Keynes's admonition against the finance theory of his day—"I accuse the classical economic theory of being itself one of these pretty, polite techniques which tries to deal with the present by abstracting from the fact that we know very little about the future" (Keynes 1937, p. 214)— is too polite for what passes for finance theory today. Its modern-day rendition is ""I accuse Modern Finance Theory of being itself one of these ugly, rude techniques which tries to deal with the present by pretending that we can predict the future". An alternative theory is desperately needed.
A Credit-based theory of Asset Prices
A major reason why the CAPM is wrong, in addition to its fantastically false assumptions, is that it ignores the role of credit as a component of aggregate demand. The proof that credit is part of aggregate demand and income (developed using Moore Tables in Chapter 10) means that there is an overlap between macroeconomics and finance, since credit today is primarily used to finance, not investment and consumption, but speculation on the value of nonfinancial assets. Therefore, credit is a major component of the demand for assets, and particularly for housing. We need a model of asset pricing that includes the role of debt. Given the growth in levered speculation on house prices over the last thirty years, this is especially needed to explain house price dynamics.
Since mortgages in advanced economies account for of the order of 70% and above of the purchase price of a house, at a first pass, one can assume that the monetary demand for housing is equal to the change in the level of mortgage debt. Using HD$ for aggregate housing demand in money terms, and DM for mortgage debt, this yields:
Using HD for demand for physical houses per year, and HP for the price of a "representative" house, then the demand for housing in terms of houses per year is:
The annual supply of housing HS consists of the time-varying fraction of the existing housing stock QH that is put up for sale, plus the net creation of new houses per year:
Since the housing stock varies much more slowly than debt, for simplicity we can drop the rate of change of the housing stock term and consider simply the proportion of existing houses offered for sale. If price adjusted instantaneously to match the physical flows of supply and demand, then I could write:
So that PH would be given by:
Treating the rates of change of and HQ as negligible, this implies that the rate of change of house prices is related to—and largely driven by—the acceleration of mortgage debt:
This relationship is confirmed by the data—see Figure 59 (where the differentials have been normalized by dividing by the House Price Index and GDP respectively). Though the correlations of both Household Debt to the House Price Index and household credit to change in the House Price Index are both positive, the largest correlation unaffected by collinearity is between the second difference of household debt and the first difference of house prices.
Figure 59: The relationship between household debt and house prices
Finance, and banking, and macroeconomics, are therefore integrated topics: they cannot be treated as separate domains, as Neoclassical treats them. My focus in this book is on how macroeconomics and the theory of banking need to be overhauled, and a similar overhaul is needed of finance theory. I won't attempt that here, but fortunately, that process has been started by a group of mathematicians in the London Mathematical Laboratory. They are developing what they call "Ergodicity Economics" to replace the existing theory of finance.
Ergodicity Economics
A representative exam question in an introductory course in finance is the following:
You have a choice between two outcomes. Which should you choose:
Receive $100 with certainty?; or
Take a 50% chance of receiving $150, and a 50% chance of receiving $60?
This is a choice between hanging onto $100, or gambling with it, and according to mainstream finance theory, you should take the gamble. This is because the expected value of option (B), the gamble, is greater than $100: the sum of 0.5 times $150 plus 0.5 times $60 is $105. If you choose option (A) in a mainstream finance exam, you will be failed.
But, according to Ergodicity Economics, this gamble isn't worth taking.
Why? Imagine that a casino offers a deal: you can either do this gamble at one point in time across 100 different tables, or you can put $100 down on one table, and play the game 100 times. The casino calls the first offer gambling across space, and the second gambling across time.
If you're a rich man, you might take gambling across space to save time. You put $100 down on each of 100 different tables, where a croupier tosses a fair coin: heads you get $150, tails you get $60. If you win on 50 tables and lose on the other 50, then you get $150 from each of the 50 winning tables ($7,500), and $60 from each of the 50 losing ones ($3000). Your $10,000 gamble across space turns into $10,500, and you're $500 ahead: easy money!
But what if you're not rich enough to wager $10,000 at one point in time? Say you only have $100 to spare, so you instead decide to choose the across time gamble, by putting $100 down on one table, and then risking your pot 100 times.
Will you get the same outcome? A Neoclassical economist might tell you so—for example, to paraphrase the prominent Neoclassical climate change economist Richard Tol (whom we'll meet in the next two chapters), "if a relationship does … hold for … variations over space, you can … confidently assert that it holds over time".
But unfortunately, you won't get the same outcome—far from it, In fact. if you win 50 times and lose 50 times—exactly the same ratio that won the wealthy gambler $500 across space—you will end up losing $99.48. $100 in, 52 cents back: you lose big time.
The reason for this drastically different outcome is that what you get in the sequential gamble is not the sum of your gambles, but the product.
Let's say that the croupier simply cycles between heads and tails, fifty times. In the first toss, you've put down $100 and you get back $150. Your next toss multiplies the $150 by 0.6, which gives you $90—you're down $10. The next pair of tosses sees you turn $90 into $81, and so on. After 50 pairs of winning and losing tosses, you have turned your $100 into 52 cents.
In the across space version of this gamble, you come out ahead on average: the odds of 50 or more wins is 1 in 2. You'd be a fool to turn this gamble down. But in the across time version, to come out ahead in this gamble, you would need to win not 50% of the time, but 56% or more of the time. The odds of that are less than 1 in 5. You'd be a fool to take this gamble.
So, which situation is more realistic as a model of investment behaviour—gambling across space, or across time? The obvious answer is that gambling through time is more realistic. As Ole Peters put it, the second example corresponds to "what will happen to my physical wealth as time goes by", whereas the former "physically corresponds to pooling and sharing among many entities" (Peters 2019, p. 1218).
The technical term for a process whose average across space is the same as its average across time is that it is ergodic. The fact that as simple a process as tossing a coin is non-ergodic shows just how rare ergodic processes are in economics. And yet, as Peters observes, Neoclassical economics makes "an indiscriminate assumption of ergodicity":
The ergodic hypothesis is a key analytical device of equilibrium statistical mechanics. It underlies the assumption that the time average and the expectation value of an observable are the same. Where it is valid, dynamical descriptions can often be replaced with much simpler probabilistic ones—time is essentially eliminated from the models. The conditions for validity are restrictive, even more so for non-equilibrium systems. Economics typically deals with systems far from equilibrium—specifically with models of growth. It may therefore come as a surprise to learn that the prevailing formulations of economic theory—expected utility theory and its descendants—make an indiscriminate assumption of ergodicity. (Peters 2019, p. 1216. Emphasis added)
Fortunately, as Peters and his colleagues demonstrate, it is possible to abandon the ergodic hypothesis and make quantitatively informed decisions in finance. This also applies to treating uncertainty in investment properly, rather than assuming uncertainty away as the CAPM does.
Investment under uncertainty
A common rule of thumb in working out whether an investment is worth undertaking is to estimate its payback period—the length of time after which the estimated cash flow from an investment will equal its costs. The mathematician John Blatt pointed out that the cavalier treatment of time in Neoclassical economics leads it to deride the period for not taking into account the time value of money, when in fact it encapsulates the most important aspect of time: uncertainty about the future (Blatt 1979; 1983, pp. 243-299).
The conventional "time value of money" approach to estimate whether a project with initial investment costs II is worthwhile is to discount future cash flows C by a rate of time preference r. To handle uncertainty, an additional term u is added to the discount:
Blatt observed that, although uncertainty about the future cannot be calculated, the more time goes on, the higher uncertainty will become. Therefore, a first pass to handle uncertainty is to assume that it grows linearly with time, so that the uncertainty-adjusted discount rate is not but . Blatt shows that the uncertainty-adjusted estimate of the value of an investment is:
Blatt then demonstrates that u can be related to two subjective estimates: the maximum time M that a firm deems as acceptable to recoup its initial investment, and the probability D that some form of disaster will strike before this time:
From this, the required payback period on an investment T is:
The payback period will therefore rise as economic conditions improve and fall as they worsen. This is yet another feature of real-world microeconomics—the behaviour of individual firms and investors—which is dominated by a macroeconomic issue: the perceived state of the future of the economy, summed up in the degree of optimism or pessimism that investors and firms have about the future. The rise of the payback period during booms, and its fall during slumps, thus produces part of the instability that drives the cyclical behaviour of the macroeconomy.
Conclusion
The topics discussed thus far in this book are, in Donald Rumsfeld's classic phrase, "known unknowns" for mainstream economics: these are factors that they acknowledge are important, but for which they have provided either wrong answers or no answers at all. All of these can be turned into known knowns by abandoning the false foundations of Neoclassical economics.
However, there are also the "unknown knowns" of mainstream economics: things about which they are ignorant, but which are of profound importance to the existence of civilisation. Here the arrogant ignorance of mainstream economics has led civilisation into an existential cul-de-sac from which there may be no escape.