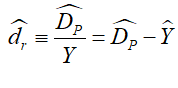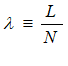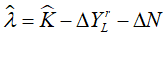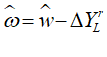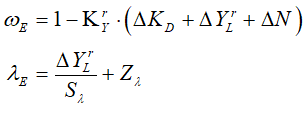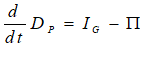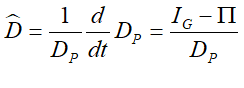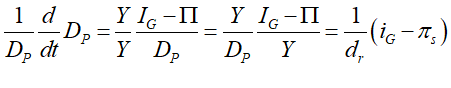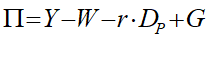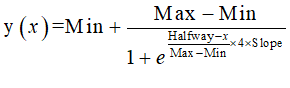The Macrofoundations of Macroeconomics

Chapter 7 from Rebuilding Economics from the Top Down

I share Blanchard's vision that "The pursuit of a widely accepted analytical macroeconomic core, in which to locate discussions and extensions, may be a pipe dream, but it is a dream surely worth pursuing". But he—and Neoclassical economics in general—err with the false belief that "Starting from explicit microfoundations is clearly essential; where else to start from?" (Blanchard 2016a, p. 3). The answer to Blanchard's purportedly rhetorical question is that the proper foundation of macroeconomics is not microeconomic theory, but macroeconomics itself.

This is Chapter 7 from my forthcoming book Rebuilding Economics from the Top Down, which will be published by the Budapest Centre for Long-Term Sustainability and the Pallas Athéné Domus Meriti Foundation. I am serialising the book chapters here.

A watermarked PDF of the manuscript is available to supporters.

This may sound paradoxical: how can your foundations be what you are trying to build on those foundations? But in fact, macroeconomic definitions which all economists must accept—simply because they are both true by definition, and essential to the study of the macroeconomy—can easily be turned into dynamic statements that enable the development of a realistic macroeconomic dynamics.

This process of building macroeconomics from macroeconomic definitions yields simple models which fit the data with far less use of arbitrary parameters than Neoclassicals impose on their "microfounded" models—and no use at all of carefully calibrated "exogenous shocks"—and which can be easily extended and made more realistic by adding further definitions (Keen 2020c).

Since this chapter (and the models in it) is necessarily complex, I'll start with its key takeaways. Working directly from incontestably true macroeconomic definitions, it is obvious that:

• Capitalism is an inherently cyclical (and evolutionary, rather than equilibrium) system;

• It is liable to collapse into a debt-deflation; but

• It can be stabilized by counter-cyclical government spending.

These conclusions are the opposite of the a priori biases of Neoclassical microeconomics. And, these results are derived from definitions that all economists must accept, which are turned into dynamic models using empirically realistic simplifying assumptions. The contrary Neoclassical beliefs that capitalism tends towards equilibrium, that debt-deflations are impossible given the (as usual, false) assumptions of the Loanable Funds model of banking, and that government intervention almost always makes the social welfare outcome worse, are based on foundations that are rotten, both intellectually and empirically.

Inherent Complexity and Cyclicality

Though, as noted in Chapter 3, three dimensions are needed to generate a fully complex system, two fundamental definitions are sufficient to demonstrate how different this approach is to Neoclassical modelling—and how realistic it is as well. These two definitions are the employment rate, and wages share of GDP: the former characterises the level of economic activity, and the latter the distribution of income.

The employment rate is how many people are employed, divided by the population; the wages share of GDP is the total wage bill, divided by GDP. Using  for the employment rate, L for employment, N for population (because I'll later use P for Prices),  for the wages share of GDP, W for total wages, and Y for GDP, the starting definitions for a genuinely well-founded macroeconomics are:

and

Applying the rules discussed in the previous chapter to Equation yields:

The same operation applied to Equation yields:

These two equations make two extremely simple, and obviously true, dynamic statements:

• The employment rate will rise if employment rises faster than population; and

• The wages share of GDP will rise if total wages rise faster than GDP.

Deriving a dynamic model from these true-by-definition statements is a straightforward task that I have put in an Appendix, so that I can focus here on the essential point that a realistic and inherently cyclical macroeconomic model can be derived directly from macroeconomic definitions which are beyond dispute.

Developing this model required the introduction of several parameters, and their names were chosen so as to make interpreting their meaning relatively easy: K_Y^r is the Capital to Output ratio, for example. The names, meanings and values of all the parameters in this model are given in Table 4.

Table 4: Parameters in the models

The model derived from these two definitions is shown in Equation :

There's are many programs that can simulate this model, from mathematical systems like Mathematica and Maple, to system dynamics programs like Vensim … and Minsky.40F I use Minsky because (a) I invented it; (b) it's free; and (c) it's the only program designed to model the dynamics of money, which becomes critically important in subsequent chapters.

The model is inherently cyclical, as Figure 9 illustrates.

Figure 9: Inherent and endemic cycles in a definitions-based dynamic macroeconomic model

Capitalism is therefore at its core a cyclical, rather than an equilibrium system. The Neoclassical portrayal of capitalism as a system that always returns to equilibrium after a disturbance is both a relic of the 19^th century belief that equilibrium was an unfortunate but necessary assumption needed to enable modelling (Jevons 1888, p. 93—a belief which ceased to be valid in the mid-20th century),41F and a characteristic that Neoclassicals artificially impose on their RBC and DSGE models, because they have elevated equilibrium from a modelling compromise into a critical component of their vision of capitalism as a welfare-maximizing system—which it isn't.

Given that this model can be derived directly from macroeconomic definitions, with none of the arbitrary assumptions that characterized Ramsey's derivation of his growth model—let alone the crazy assumptions added by later Neoclassicals to apply Ramsey's model to the macroeconomy (Solow 2010, p. 13)42F—this model should be regarded as half of the foundational model of macroeconomics—half because it does not yet include the financial sector or the government, which I add in the next two sections.

This model is, in fact, Richard Goodwin's "growth cycle" model, which he developed in 1965 (Goodwin 1966; Goodwin 1967). My sole contribution here is to show that, rather than being based on "ad-hoc" equations, Goodwin's model can be directly and easily derived from strictly true macroeconomic definitions, and straightforward simplifying assumptions.

Goodwin's model has been neglected in economics, largely because Neoclassical economists abhor non-equilibrium systems, but also because an unfortunate paper—for which I must confess that I was one of the referees who recommended its publication—incorrectly derided its empirical accuracy. Entitled "Testing Goodwin: Growth Cycles in Ten OECD Countries", it concluded that "At a quantitative level, Goodwin's … estimated parameter values poorly predict the cycles' centres" (Harvie 2000, p. 359).

In fact, this conclusion was due to a mistake by Harvie that he later frankly described to me as a "typical schoolboy error": he used numbers in percentages, when his work had been done in fractions. That put his numbers out by a factor of 100—a fact that I only discovered when I attempted to use his parameters in a model.43F This mistake was corrected by (Grasselli and Maheshwari 2017), who found that the properly calibrated model was consistent with the data for OECD countries.

Figure 10 illustrates this with respect to US data from 1948 till 1968: using historically reasonable parameter values, the equilibrium of the model in Figure 9 precisely reproduces the average value for the employment rate and wages share between 1948 and 1968,44F even though the model is still very incomplete.^,45F The model also reproduces the cyclicality (though not the actual magnitude of those cycles) of the empirical data—something that a Neoclassical model cannot do without adding (carefully calibrated!) "exogenous shocks".

Figure 10: USA Employment and Wages Share Dynamics from 1948 till 1968

The next section completes this as a model of a pure capitalist economy46F by introducing the financial sector, in the form of the private debt to GDP ratio (in a later chapter, I explain why private debt is an essential component of the foundational model of macroeconomics).

Debt-Deflation in a Pure Credit Economy

The debt ratio d_r is the level of private debt (D_P) divided by GDP:

In dynamic form, this definition is:

As usual, this equation has a straightforward verbal interpretation, that the private debt ratio will rise if private debt grows faster than GDP.

Several modifications are required to variables in the previous model to integrate private debt dynamics into it. Debt means interest payments, so the rate of interest r was added as a parameter (it can be a variable in more elaborate models); profit is now net of interest payments as well as of wages; and Goodwin's extreme assumption that capitalists invest all their profits is replaced by an investment function i_G, (based on the rate of profit _r) which has the same form as the wage change function in the previous model, and which assumes—rather too generously—that all debt is used to finance productive investment.47F As explained in the Section 7.6, this results in the following 3-equation system:

Here g_r stands for the growth rate; w stands for the wage change function; i_G stands for gross investment (investment before depreciation) and is a function of the rate of profit; and the profit share _s is introduced, since it plays a significant—and surprising—role in the dynamics of the model.

The parameters for the investment function, and the interest rate, are shown in Table 5.

Table 5: Parameters added to the Goodwin model to include private debt

With this model, "we're not in Kansas anymore",

48F when compared to the Neoclassical view of reality. The model can reach equilibrium, but most likely it will not. It will appear to be heading for equilibrium, only to cycle away from it (Pomeau and Manneville 1980). The people who don't borrow in this simple model—workers—are the ones who pay the cost of borrowing, via a lower share of national income. The people who do borrow—capitalists—don't pay the cost, but they are also the last ones to realise that, when the system is unstable, it is headed for a breakdown that will bankrupt them. Finally, the direct beneficiaries of rising private debt—bankers—end up owning everything of nothing.

The technical reason for this much greater complexity of this model over Goodwin's is the fact that a model needs three dimensions in order to display complex behaviour—"Period Three Implies Chaos", as Li and Yorke put it (Li and Yorke 1975). Goodwin's model, with just two dimensions (the employment rate  and the wages share ), is constrained by the nature of differential equations to display a very limited range of dynamic behaviours. But when the third dimension of the private debt ratio d_r is added, much more complex and realistic behaviours can be generated.

Figure 11 shows a run of the model that does converge to equilibrium (though very slowly).49F

Figure 11: The model with investment and capital to output parameters that lead to equilibrium

With the parameter values used in Figure 11, the new system-state in this model—the level of private debt—has an equilibrium which is comparable to the level of the 1950s. But as Figure 12 illustrates, this was no equilibrium: the ratio rose substantially, and normally constantly, until hitting a peak of 170% of GDP in 2008.

Figure 12: USA Private Debt level since WWII (https://data.bis.org/topics/TOTAL_CREDIT)

If we choose parameter values for the model that generate this peak level of private debt as an equilibrium—by changing the slope of the investment function from 5 to 5.86—then we get an entirely different class of dynamics from this model. What Costa-Lima and Grasselli characterized as the "good equilibrium" of this model (Costa Lima et al. 2014, p. 35) becomes an unstable "strange attractor", while the "bad equilibrium" becomes a stable attractor: the model eventually collapses into zero wages share, zero employment, and an infinite debt ratio.

One emergent property of this model is that, with parameter values that lead to a private debt crisis, the volatility of the model declines prior to the crisis, in a manner which was replicated by the real world in the "Great Moderation" that preceded the "Great Recession" of 2007. This phenomenon is more obvious with nonlinear behavioural functions, which are applied in the model shown in Figure 14, which uses the nonlinear functions shown in Figure 13. These are generalized exponentials, give a consistent curvature, and rule out anomalies like negative investment that a linear function will generate. I've used linear functions for workers' wage demands and capitalist investment decisions thus far, not because they're more realistic—far from it—but because their use confirms that the cyclical behaviour of the models is driven, not by assumptions imposed by the modeller, but by the structure of the economy itself.

Figure 13: Nonlinear versus linear functions for wage change, investment and government spending change

With these functions and parameter values, the pure credit model undergoes a debt-induced crisis, as shown in Figure 14.

Figure 14: A Private-Debt-induced Crisis with a nonlinear investment function

This still very simple and stylized model has an important real-world implication, which I noted in the conclusion to my first paper on this topic, "Finance and Economic Breakdown: Modelling Minsky's Financial Instability Hypothesis" (Keen 1995b): a period of tranquillity in a capitalist economy is not inherently a good thing, but can in fact be a warning that a crisis is approaching:

From the perspective of economic theory and policy, this vision of a capitalist economy with finance requires us to go beyond that habit of mind that Keynes described so well, the excessive reliance on the (stable) recent past as a guide to the future. The chaotic dynamics explored in this paper should warn us against accepting a period of relative tranquility in a capitalist economy as anything other than a lull before the storm. (Keen 1995b, p. 634. Emphasis added)

In contrast, equilibrium-obsessed Neoclassical economists saw the "Great Moderation" as a "welcome change to the economy" (Bernanke 2004), and actually attributed it to their successful management of the economy:

The sources of the Great Moderation remain somewhat controversial, but as I have argued elsewhere, there is evidence for the view that improved control of inflation has contributed in important measure to this welcome change in the economy. (Bernanke 2004. Emphasis added)

The other emergent property of the model is equally striking: though firms (capitalists) are the ones doing the borrowing in this model, it is the workers who pay for rising debt via a declining workers' share of income. Profits cycle around the equilibrium level until the crisis, while workers' incomes decline as a direct effect of the rising income share going to banks.

This model is, of course, a mathematical rendition of Hyman Minsky's "Financial Instability Hypothesis" (Minsky 1975, 1982). Though other specialists on Minsky emphasise his classification of finance into Hedge, Speculative and Ponzi Finance, and the change in the relative proportions of these financial archetypes through the business cycle, my favourite expression of the FIH as a dynamic process is the following from "The Financial Instability Hypothesis: An Interpretation of Keynes and an Alternative to 'Standard' Theory":

The natural starting place for analyzing the relation between debt and income is to take an economy with a cyclical past that is now doing well. The inherited debt reflects the history of the economy, which includes a period in the not-too-distant past in which the economy did not do well. Acceptable liability structures are based upon some margin of safety so that expected cash flows, even in periods when the economy is not doing well, will cover contractual debt payments.

As the period over which the economy does well lengthens, two things become evident in board rooms. Existing debts are easily validated and units that were heavily in debt prospered; it paid to lever. After the event it becomes apparent that the margins of safety built into debt structures were too great. As a result, over a period in which the economy does well, views about acceptable debt structure change. In the deal-making that goes on between banks, investment bankers, and businessmen, the acceptable amount of debt to use in financing various types of activity and positions increases. This increase in the weight of debt financing raises the market price of capital assets and increases investment. As this continues the economy is transformed into a boom economy…

It follows that the fundamental instability of a capitalist economy is upward. The tendency to transform doing well into a speculative investment boom is the basic instability in a capitalist economy. (Minsky 1977, pp. 12-13; 1982, pp. 66-67. Emphasis added)

Minsky's genius was his capacity to see this fundamental instability of capitalism, free of the hobbling Neoclassical assumption of equilibrium, and to relate this to the level of private debt—an insight he garnered from Fisher (Fisher 1933) rather than from Keynes, whom he didn't properly appreciate until he read the brief essay "The General Theory of Employment" (Keynes 1937) in 1968 (Minsky 1969a, p. 9, footnote 6; 1969b, p. 225).

We now have three-quarters of a foundational dynamic model of capitalism. The final element needed to complete this model (prior to the introduction of prices) is a government sector.

Stabilising an Unstable Economy

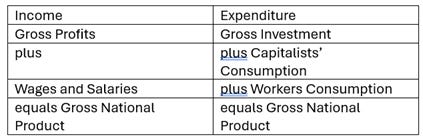
A government sector is added by applying Kalecki's insight that net government spending adds to profits. Kalecki began with Table 6, which shows GDP in terms of both income (the left-hand column) and expenditure:

Table 6:Kalecki's basic Income and Expenditure Identity (Kalecki 1954, p. 45)

Assuming that workers spend all of their incomes, Kalecki equated Gross Profits to the sum of Gross Investment and Capitalists' Consumption, and then asked the causal question: which comes first? His answer was that:

it is clear that capitalists may decide to consume and to invest more in a given period than in the preceding one, but they cannot decide to earn more. It is, therefore, their investment and consumption decisions which determine profits, and not vice versa. (Kalecki 1954, p. 46. Emphasis added)

Kalecki then included government expenditure and taxes and exports, and allowed for some saving by workers. Simplifying his final equation somewhat, this led to the relationship that:

The model in this section follows Kalecki (Kalecki 1954, p. 49) by redefining profit to include net government spending (spending in excess of taxation), adds an equation for the rate of change of net government spending as a function of the level of unemployment, and a differential equation for government net spending:

This creates a pseudo-4-dimensional model:

Figure 15 simulates this system with nonlinear behavioural functions and the same system parameters as the unstable private-sector-only model in Figure 14, to illustrate the result that, as Hyman Minsky argued, "big government virtually ensures that a great depression cannot happen again" (Minsky 1982, p. xxxii). However, the process is more complex—fittingly—than Minsky could envisage with purely verbal reasoning.

The definitive treatment of the dynamic and stability properties of this model is given by Costa-Lima, Grasselli et al. in "Destabilizing a stable crisis: Employment persistence and government intervention in macroeconomics" (Costa Lima et al. 2014), though their model was more complicated than the one shown here.

The obvious outcome that the model remains cyclical, but does not undergo a breakdown, is due to a characteristic of complex dynamic systems known as persistence. Given the commonality of this phenomenon in real-world systems, and the unfamiliarity of economists with this concept, it is worth quoting their paper at length:

Persistence theory studies the long-term behaviour of dynamical systems, in particular the possibility that one or more variables remain bounded away from zero. Typical questions are, for example, which species in a model of interacting species will survive over the long-term, or whether it is the case that in an endemic model an infection cannot persist in a population due to the depletion of the susceptible population.

In our context, we are interested in establishing conditions in economic models that prevent one or more key economic variables, such as the employment rate, from vanishing… we prove … that under a variety of alternative mild conditions on government subsidies, the model describing the economy is uniformly weakly persistent with respect to the employment rate …

[W]e can guarantee that the employment rate does not remain indefinitely trapped at arbitrarily small values. This is in sharp contrast with what happens in the model without government intervention, where the employment rate is guaranteed to converge to zero and remain there forever if the initial conditions are in the basin of attraction of the bad equilibrium corresponding to infinite debt levels… no matter how disastrous the initial conditions are, a sufficiently responsive government can bring the economy back from a state of crises associated with zero employment rates…

On the other hand … austerity implies that the government cannot prevent the economy from remaining trapped in the basin of attraction of at least one of the bad equilibria, which is of course an undesirable outcome. (Costa Lima et al. 2014, pp. 31, 37. Emphasis added)

Figure 15: Net government spending stabilizes the previously unstable system

Conclusion

Though these models are still very simple, they generate a picture of the economy that is at once totally different to the Neoclassical fantasy of eternal (but sometimes exogenously shocked) equilibrium, and empirically much easier to fit to actual data. In Chapter 9, I show that these models can also be developed by following the causal approach of system dynamics, which also make it easier to add further real-world complexities to the basic models. Blanchard's dream of "a widely accepted analytical macroeconomic core, in which to locate discussions and extensions" is alive and well, but only if the dead-end of Neoclassical equilibrium modelling is abandoned.

There are only two issues left for these foundational and definitional models: the role of prices, and the justification for treating private debt as an essential component of a fundamental model of macroeconomics. I tackle these issues in the next three chapters.

Appendix: Deriving Goodwin's model from macroeconomic definitions

The employment rate is the number of people with a job, divided by the population; the wages share of GDP is the total wage bill, divided by GDP. Using  for the employment rate, L for employment, N for population (because later I'll use P for Prices),  for the wages share of GDP, W for total wages, and Y for GDP, my starting definitions are:

And

Applying the rules discussed in the previous chapter to Equation yields:

And the same to Equation yields:

At this point, we are dealing with truisms. To turn these statements into a basic economic model, we need to add some more definitions, and a handful of genuine simplifying assumptions.

Now a quick note on notation: mathematical equations are compact because of the use of symbols, but the symbols can be confusing. To minimize this problem, where possible, I use symbols with superscripts and subscripts that make intuitive sense. The first example here is the ratio of capital (as in machines, rather than money) to output. The economic convention is to use K for capital and Y for output. I therefore use "K" with the subscript "Y" and the superscript "r" to indicate the "Capital to Output ratio":

Similarly, the output to labour ratio is "Y subscript L superscript r":

We use these definitions to expand the terms in Equation and . I'll work with the equation for the rate of growth of the employment rate first.

Firstly, replacing in Equation with yields:

Replacing with yields:

At this stage, we're still working with truisms. To progress further, we have to introduce simplifying assumptions. The simplest terms to work with in Equation are the rate of growth of population, and the rate of growth of the output to labour ratio, which I replace with constants. This amounts to assuming constant population growth at the rate of N ("change in Population") per year:

I also assume constant technical progress ("Change in the Output to Labour Ratio"), which is represented by a higher level of output per worker over time:

In future chapters, I'll replace this—in my considered opinion—deceptive concept of what technical progress means, with a rising capital to labour ratio, which, as I will show, is more realistic. But for simplicity in this chapter, I'll stick with the customary treatment of rising productivity as signifying a rising output to labour ratio. So, at this stage, our equation for the rate of change of the employment ratio is:

Next, we have the rate of change of the capital to output ratio . The discovery, by Leontief, that this ratio was fairly constant for most countries—see
Figure 16—led to the "Leontief Production Function", in which output is assumed to be equal to capital divided by a constant capital to output ratio. Neoclassicals like to ridicule this in comparison to their "Cobb-Douglas Production Function", which allows for a flexible relationship between capital and labour in producing output, but as I'll show in Chapter 13, there is a very solid causal relationship underlying the concept—and reality—of a relatively constant capital to output ratio.

Figure 16: Capital output ratios for a range of high-income economies with advanced manufacturing sectors

The simplifying assumption that the capital to output ratio is a constant means that its rate of change is zero:

This means that, when we use the capital to output ratio, we can treat it as a parameter rather than a variable:

Equation thus simplifies to just three terms, rather than four:

Since the ratio of capital to output is a constant, the rate of growth ratio of output is the same as that for capital:

Therefore, the only term left to define is , which is the rate of change of the capital stock:

The rate of change of the capital stock is the level of net investment , divided by the capital stock. Net investment is gross investment minus depreciation, and the standard assumption—supported by empirical data—is that depreciation is a constant fraction of the capital stock ("Change in Capital due to Depreciation"). Finally, from Equation , K can be replaced by Putting these all together enables us to express the rate of change of the capital stock in terms of gross investment divided by the capital to output ratio times output, minus the rate of depreciation:

This is also the rate of growth of GDP:

Our model for the rate of change of the employment rate is now:

That leaves just one term to define: gross investment. Here I will use an extreme simplifying assumption from Richard Goodwin—which we'll shortly relax—that capitalists invest all their profits (Goodwin 1967):

In this two-class model—workers earning wages, and capitalists earning profits—it follows that profits are equal to output Y minus total wages W.

Therefore, at this stage of developing the model, we assume that gross investment equals Output minus Wages. Substitute that into Equation yields:

The first term factors to, since . We now have the first of the two differential equations in this foundational model of capitalism:

Remembering that , we can now multiply both sides of Equation by to yield:

This was a lengthy process to explain, but it's much simpler than the "hard slog" Neoclassicals have to undertake, as Blanchard rightly described the process of deriving a DSGE model from microeconomics.

This equation also points out an immediate difference—and improvement—of this approach to macroeconomics. There is an inherent nonlinearity in the model, in that the equation for the rate of change of the employment rate includes the employment rate, multiplied by the negative of the wages share of GDP. Unlike Neoclassicals, who run away from nonlinearity because it makes solving their "rational expectations"50F terms so difficult, nonlinearity is an essential and realistic element of a dynamic, far-from-equilibrium model of capitalism.

Next, we have to convert the ratio of rate of change of wages share into a dynamic equation. We start from:

If we assume a common wage rate w, we can expand this to:

L can be replaced by output divided by the output to labour ratio:

The output terms cancel, leaving us with an equation that has an easy and meaningful verbal interpretation: the wages share of GDP will rise if the real wage rises faster than the rate of technical progress:

Now, since we need an expression for the rate of change of wages ratio, we must confront the vexed topic of "the Phillips Curve".

Appendix: The "Phillips Curve"

Bill Phillips was an engineer before he became an economist, and his intention in developing the Curve that bears his name was to empirically justify an assumption he had made in what was the world's first system dynamics model applied to economics—see Figures 10 and 11 in (Phillips 1954, pp. 306, 308)—that the rate of change of prices was a rising nonlinear function of the level of production:

We may therefore postulate a relationship between the level of production and the rate of change of factor prices, which is probably of the form shown in Fig. 11, the fairly sharp bend in the curve where it passes through zero rate of change of prices being the result of the greater rigidity of factor prices in the downward than in the upward direction. (Phillips 1954, p. 308)

Phillips himself was a critic of how his Curve was used (Leeson 1997, 1998a, 1998b), and his function was much richer than the caricature which has generally made its way into the modelling literature. His model of how money wages are determined had not just one factor—the rate of unemployment—but three: the rate of unemployment, its rate of change, and imported "cost-push" inflation (Phillips 1958, p. 298):

When the demand for a commodity or service is high relatively to the supply of it we expect the price to rise, the rate of rise being greater the greater the excess demand … It seems plausible that this principle should operate as one of the factors determining the rate of change of money wage rates …

The relation between unemployment and the rate of change of wage rates is therefore likely to be highly non-linear…

a second factor influencing the rate of change of money wage rates might be the rate of change of the demand for labour, and so of unemployment…

A third factor which may affect the rate of change of money wage rates is the rate of change of retail prices, operating through cost-of-living adjustments in wage rates… (Phillips 1958, p. 283. Emphasis added)

The proper Phillips "Curve" is thus both nonlinear in unemployment, and 3-dimensional. However, for the sake of simplicity here—prior to getting more realistic in later models—I will use 1-dimensional and linear function in this initial model, but using the rate of employment rather than the rate of unemployment. With only 53 annual data points, and a steep nonlinearity as unemployment approached zero (Phillips 1958, Figure 1, p. 285), Phillips was forced to use an asymptotic function, to make it impossible for the unemployment figure to turn negative. By using the ratio of employment to population as my input, rather than the rate of unemployment, I avoid this last problem for a linear function. The employment ratio in the USA ranges between 55% and 65%—see Figure 17.

Figure 17: The employment ratio for the USA. See https://fred.stlouisfed.org/series/EMRATIO

Since the Phillips Curve gives us the ratio of the rate of change of wages, we can write:

Here S_ is the slope of the Phillips Curve, and Z_ is the employment level at which the rate of change of wages is zero. This now gives us our second fundamental dynamic equation:

In standard differential equation form, this is:

This equation, like the one for the employment rate, has a fundamental nonlinearity, that the wages share of GDP is multiplied by the employment rate. Using w for the wage change function shown in Equation , the full system is:

We can now define the equilibria for this system. One is ==0, but the meaningful one is where:

Calling the values that cause Equation (44) to be true _E and _E, these equilibrium values are:

Appendix: Deriving Minsky's Financial Instability Hypothesis from Definitions

A few generalisations are needed to enable private debt to be added to this model. Firstly, Goodwin's extreme assumption that capitalists invest all their profits needs to be replaced by an investment function, in which capitalist investment is determined by the rate of profit. Capitalists will then invest more than their profits above a target rate of profit, which necessitates borrowing from banks to cover the difference. When profit is below this level, capitalists pay down their outstanding debt.

Secondly, the rate of profit needs to be redefined to take into account the payment of interest on outstanding debt.

Net profit is now output minus wages minus interest on outstanding debt, where r is the rate of interest on private debt:

The profit share of GDP is profit divided by GDP:

The rate of profit is profit divided by capital:

Gross investment is now a function of the rate of profit, while the investment ratio is gross investment divided by GDP:

        
For simplicity, I use the same functional form as for the wage change function, but with different arguments.

With these definitions, we are ready to derive an equation for the rate of change of private debt. We start, as always, with the rate of growth of the debt ratio:

As usual, this has a simple interpretation: the private debt ratio will rise if private debt rises faster than GDP. The rate of growth of GDP in terms of the investment ratio i_G is:

Therefore, all we have to do is expand . I make the simplifying assumption that only firms (or capitalists) borrow, and that investment in excess of profits is financed by debt.51F Therefore:

Using this to expand :

We can simplify this equation by multiplying the right-hand side by Y/Y and rearranging terms:

We can now insert this into Equation (64):

Putting this in differential equation form:

The full system of equations is:

To make the equation easier to read, I have used two additional collective terms: g_r for the growth rate, and w for the wage change function ("Phillips Curve"):

The behaviour of this model is best illustrated using nonlinear behavioural functions, as shown in Figure 13. The cycles first diminish in size—a "Great Moderation"—and then they start to get larger. Technically, the "good equilibrium" of the model is a "strange attractor" which attracts the system from a distance but then repels closer up when the linear components of the system start to dominate the nonlinear components. The system is then cyclically repelled from the "good equilibrium" until it falls into the basin of attraction of the "bad equilibrium" of zero employment, zero wages share and an infinite debt ratio.

Figure 18: A debt crisis with nonlinear behavioural functions

Appendix: Adding a Government Sector

We start from Kalecki's proof that the government deficit is part of gross profits (Kalecki 1954, p. 49), so that Equation now becomes:

Here G represents the excess of government spending over taxation. The rate of profit now includes g_s, the deficit as a fraction of GDP:

The rate of change of net government spending G is a function of the rate of employment:

In this simple model, I relate government spending to the rate of employment. However, as I noted in (Keen 1995b), real governments, under the influence of Neoclassical economic thought,     have not lived up to this Keynesian ideal of trying to stabilize the economy around a target employment rate. The consequence is that the 2007 global financial crisis actually occurred, despite the fact that government policy did have the capacity to "stabilize an unstable economy". This failure was predictable a decade before the crisis:

over the last thirty years, Western governments have adopted policies antithetical to the countercyclical role they largely followed in the 1950s and 1960s… they have lessened the progressiveness of income tax scales… [but] there is still a positive relation between the level of unemployment and the rate of change of the government spending to output ratio… such a form of intervention would not attenuate the investment behavior of capitalists, with the consequence that booms would be as marked as in the non-government simulation. Debt-induced breakdowns would thus still occur. Increased government spending during slumps would enable recovery in the aftermath to lesser booms; larger booms, however, could result in the rate of growth of accumulated private debt exceeding net profits for some time, thus leading to a prolonged slump. (Keen 1995b, pp. 630-632)

This model therefore simulates what would happen if a Keynesian-oriented—or in modern terms, MMT-aware—government was in control. To simulate what actually happened, you could make the target unemployment rate a function of hysteresis, or have inflation-control policies (using interest rates, which could be destabilizing rather than stabilizing, by increasing the rate of growth of private debt during a boom) overrule employment-control policies. For generality, I therefore omit the argument for the net government spending function from the following equations.

The derivation of deficit spending function is straightforward:

The full set of equations is therefore:

Appendix: Generalized Exponential and Logistic Functions

I prefer to avoid idiosyncratic functions which can determine the behaviour of a model, even more so than the actual nonlinear relationships in the model. For this reason, when necessary, I use a generalized exponential function as an alternative to a linear function, since it generates a smoothly increasing (or smoothly decreasing) function, and therefore the reactions are proportional over its entire range. The function takes 4 arguments: a pair of coordinates (x_val,y_val) through which the function passes, a slope s_val at that point, and a minimum value m_val:

Sometimes a function with a minimum and maximum value also makes sense—for example, when modelling a process like technical change as a function of the rate of growth, where there will be a minimum and a maximum feasible rate of change. This function takes the arguments Min, Max, Halfway, and Slope at the halfway point:

The values used for the generalised exponential function in the models in this chapter are shown in Figure 13.