Who could have seen this coming?
Climate chaos wasn't foreseen by economists because they used a fantasy function to predict the future
2022 is a year of undeniable climate extremes. In Pakistan, unprecedented floods have destroyed over half a million homes and put one third of the country underwater. In China, a drought with no precedent in human history, according to the global expert on extreme temperatures, is forcing semiconductor plants to close so that energy and water can be reserved for domestic use. Europe is suffering its longest drought in 500 years, with no end in sight, and facing energy prices that have risen up to sixfold in a year, with the Ukraine War only partially to blame. Drought in the USA is exposing never-before-seen dinosaur footprints in dried-up rivers.
Who could have seen this coming? Certainly not economists, who predicted that far higher temperatures than today would do only moderate damage to the economy. William Nordhaus, who was given the Nobel Prize in Economics for his work on climate change, claimed in 2018 that a 6℃ increase in global temperature would cause GDP to fall by less than 10%. But we're starting to see huge catastrophes across the globe at a temperature rise of just over 1℃. Nordhaus's predictions are starting to look spectacularly wrong, and the New York Times said so just recently in an article titled "Pace of Climate Change Sends Economists Back to Drawing Board". The author, Lydia DePillis, took direct aim at Nordhaus:
Nordhaus's model was drawing criticism for underestimating the havoc that climate change would wreak… it still relies on broad assumptions and … doesn't fully incorporate the risk of less likely but substantially worse trajectories of warming.
What Nordhaus did to make his tiny estimate of damages was take current data on temperature and GDP and extrapolate that forward to future temperatures using the second-simplest equation known to man, the "quadratic" or parabola. The simplest formula is a straight line—"", if you remember your schooldays algebra. Nordhaus's equation is "": the change in GDP thanks to global warming is a constant, multiplied by the temperature increase squared. Nordhaus's estimate of the constant was a mere 0.227%—so that a 2 degree increase in temperature would only reduce GDP by 4 times 0.227%, or less than 1%. This is a future GDP too, in the year 2100, when Nordhaus also assumed that GDP per capita would be 4-5 times larger than it is today.
I've pulled his work apart in academic papers, but what I want to do today is replicate it—and show why it is so wrong.
There's an excellent database maintained by the USA's National Oceanic and Atmospheric Administration (NOAA) called the "Billion-Dollar Weather and Climate Disasters Database". I took this data and did exactly the same thing that Nordhaus has done: fit the data using a quadratic. That yielded Figure 1. With current data, it predicts about three times the damages that Nordhaus predicted.
Figure 1: The NOAA data and a quadratic fit
But that's still small in the scheme of things: if you extrapolate it forward to 6℃, it predicts a 20% fall in GDP from 6℃ of warming. That's bigger, but it still means that GDP per capita in 2100 will be four times what it is today, versus 5 times if there were no global warming.
But a quadratic isn't the only formula you can use to forecast—and in fact, it hard to think of a less likely function than a quadratic to predict the future economic consequences of global warming. Two other far more likely candidates are an exponential and a logistic.
An exponential is what you get when you say, for example, that "the rate of population growth is 2% per year": anything expressed as a percentage rate of growth is an exponential. A logistic is more complicated: it has exponential growth, but it also has a ceiling. Figure 2 shows the fit of an exponential and a logistic, as well as a quadratic—and at current levels, you simply can't tell them apart.
Figure 2: The same chart as, but now with an exponential and a logistic fit
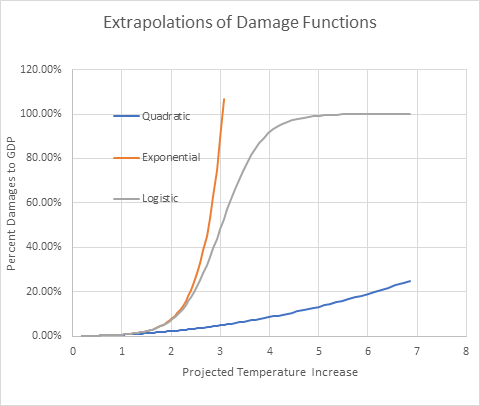
But what happens when you extrapolate past current temperatures? Then, figuratively speaking, all hell breaks loose: the exponential forecast predicts that when temperatures reach 3℃ above pre-industrial levels, all of GDP will be destroyed. The logistic is only slightly less scary—it predicts that 50% of the economy will be gone at 3℃, and all of it at 5℃.
Figure 3: Extrapolating the functions in Figure 2 out to 7℃
So which function makes more sense? It certainly isn't the quadratic, which Nordhaus and all mainstream climate change economists use: though a quadratic gets steeper as temperatures rise, it never gets steeper more quickly, as will happen when we hit climate tipping points. The logistic is the most likely fit to what's going to happen as climate tipping points add to the damage already done by rising CO2 levels.
Figure 4: The same data as in Figure 3, but plotted against time rather than temperature
That implies a scary future indeed for the remainder of the 21st century. Whereas Nordhaus's quadratic claims the damage to the economy in the 21st century would be minimal—a less than 10% fall in a per capita GDP 4-5 times higher than today's—the exponential and logistic assert that there won't be an economy by the mid to late 21st century.
These functions aren't necessarily correct, but they're certainly not as wrong as Nordhaus's trivial estimates. But if they are even close to what we are going to experience, then it's time to pull out all stops to combat global warming.