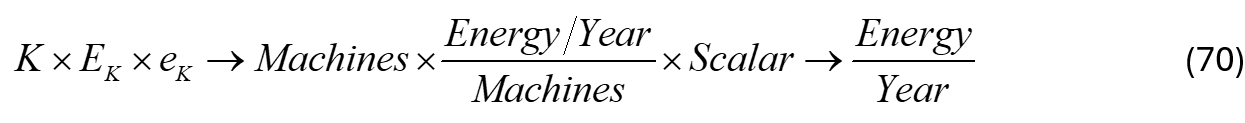The Role of Energy in Economics
Chapter 9 of Money and Macroeconomics from First Principles, for Elon Musk and Other Engineers
This book has focused upon conventional misconceptions about the nature of money, because they are the basis of Musk’s misconceived goal of eliminating the budget deficit. But money is not the only fundamental aspect of the economy that mainstream economics gets wrong: it also makes fundamental errors about the role of energy in production.
Economists use “Production functions” in aggregate macroeconomic models, which purport to relate output (Gross Domestic Product or Y) to its necessary inputs. The conventional Neoclassical model of production—known as the Cobb-Douglas Production Function (CDPF)—portrays Y as being the product of “Total Factor Productivity” (A), Labour (L) and Capital (K), where Y, A, L and K are all functions of time:
The exponents for Labor and Capital sum to one, for the sensible reason that a hypothetical doubling of all inputs should also double output. The exponent alpha represents the share of Capital in GDP, making this model of production consistent with the Neoclassical theory of income distribution, in which “factors of production” (Labour and Capital) are assumed to be paid their marginal products—see Equation 61.[1]
When the model was first calibrated empirically by its creators, they claimed that a was 0.25, which was equal to the profit share of GDP at the time (in the Appendix to this Chapter, I show that this result was spurious).
When the TFP term was introduced by Robert Solow in 1957, its time series had to be derived from data as a residual, since there was data for output (Y), Labor (L) and Capital (K), but not for Total Factor Productivity. To calculate this series, Solow simple assumed that Neoclassical theory was correct. In his words, his analysis had the price of requiring a “new assumption, that factors are paid their marginal products” and “since the latter is an assumption often made, the price may not be unreasonably high” {Solow, 1957 #7187, p. 312}.
With this assumption, he found that of the order of 87.5% of the increase in output over time was due to the increase in Total Factor Productivity. This has since become known as “The Solow Residual”.
This production function has been critiqued extensively by non-Neoclassical economists {Shaikh, 2005 #6373;Shaikh, 1987 #4796;Shaikh, 1974 #4795;Felipe, 2020 #7180;Felipe, 2014 #5783;Felipe, 2005 #5437}, but these criticisms have had no impact on the use of the CDPF, which now dominates Neoclassical models of production.[2]
An alternative model of production—first developed by Wassily Leontief (who pioneered the use of matrix mathematics in economics) —is based on the empirical regularity that output (Y), however measured, is proportional to capital (K), however measured, with the capital to output ratio being relatively constant for individual countries, with the ratio ranging between 3 and 6 for developed industrial countries—see Figure 40 for the USA’s ratio.[3]
Figure 40: The USA's capital to output ratio derived from Penn World Tables data (Series cgdpo and cn)
Called the Leontief Production Function(LPF), it is far simpler than the CDPF, in that Output is as a linear function of Capital:
There is no explicit role for energy in either production function. In this chapter, I show what happens to both production functions once energy is properly introduced.
Energy in the CDPF
By default, Neoclassical economists do not include energy at all in their models of production. When they do, they treat energy (E) as a third “factor of production” in the Cobb-Douglas Production Function. In keeping with how they model Labour and Capital, Energy has an exponent, based on the share of energy in GDP, of 0.03-0.05, {Engström, 2016 #6464, p. 555;Bachmann, 2022 #6606, p. 3}:
This attributes a trivial role to energy in production. As Bachmann et al. stated when considering the impact of a fall in the supply of energy to Germany due to sanctions on Russia, this function predicts that a 10% fall in energy would cause only a 0.4% fall in GDP:
Hence production Y declines with energy E but with an elasticity of only a. In our calibration we choose a = 0.04. Therefore, for example, a drop in energy supply of Δ log E = −10% reduces production by Δ logY = 0.025 × 0.1 = 0.004 = 0.4%
The key fallacy in this treatment of energy is that energy is not a separate “factor of production”, but an essential input for both workers (Labor) and machines (Capital), without which they can do no work. As I put it in “A Note on the Role of Energy in Production”:
labour without energy is a corpse, while capital without energy is a sculpture. {Keen, 2019 #5507, p. 41}
Therefore, the proper way to characterise production with energy is to make energy an input to both Labor and Capital, without which production cannot occur:
Obviously the forms of energy are very different for workers and machinery, but the substitutions shown in Equation can be used in an aggregative model:
Here L and K represent the number of workers and machines respectively, EL and EK the energy consumed per worker and per machine per year, and eL and eK represent the proportion of that energy which is turned into useful work.
As I explain in the Appendix to this Chapter, the original Cobb-Douglas equation did not have the A term, which was introduced by Robert Solow {Solow, 1957 #5296}. They instead used Equation , where b was a scalar:
Samuelson showed that, with the index data they used, b should have been 1 {Samuelson, 1979 #5387, p. 928}.[4] Substituting the terms in Equation into Equation without the b constant yields Equation :
This can be rearranged to Equation :
The final component of Equation is the basic Cobb-Douglas relation.
The first is the product of the energy consumed by workers, multiplied by the fraction of that energy which is applied to production. The former has risen enormously since the Industrial Revolution, while the latter has fallen as living standards have risen. The product can be treated as a constant, representing the amount of energy that an average human can output in unskilled labour over a year.
The second is the product of the energy consumed by the representative machine, multiplied by the fraction of that energy which is applied to production. The former has risen exponentially since the Industrial Revolution while the latter is a scalar which must be less than 1, and is effectively bounded by the Second Law of Thermodynamics. This gives us Equation :
This decomposition shows that what “Solow’s Residual” actually measures is the amount of energy which is converted into useful energy (exergy)[5] by the representative machine of a given time. It is therefore little wonder that “TFP” accounts for the vast majority of the increase in output, since the amount of energy processed by machine has risen so dramatically since the Industrial Revolution.
Equation gives the energy input to machines the same exponent as for Capital (customarily 0.3), whereas Neoclassical economists give it a trivial exponent (0.03-0.04). This alone means that the impact of change in energy inputs on change of output is a factor of ten larger than Neoclassical economists think.
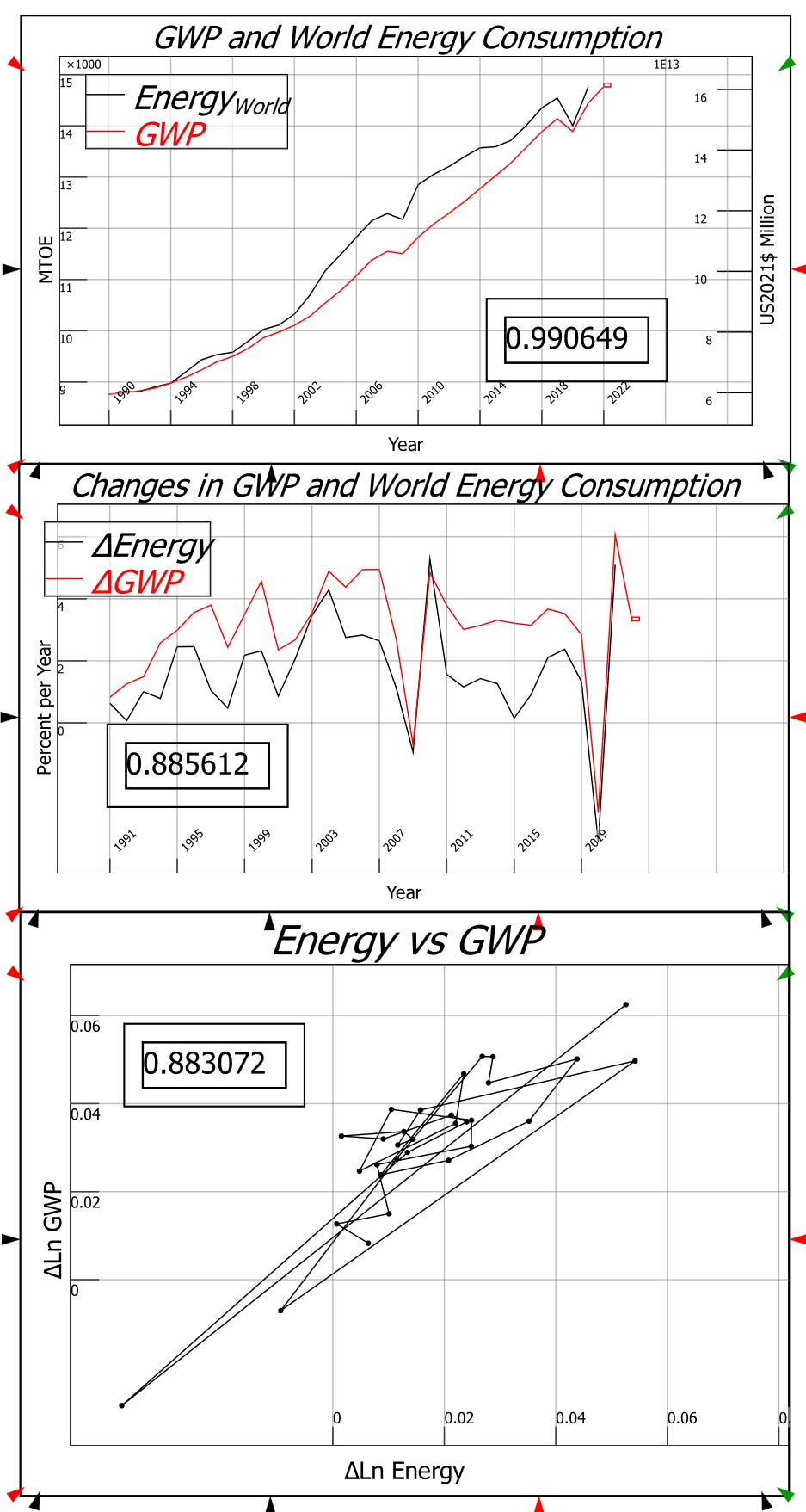
However, this modification isn’t sufficient to fit the data. An exponent of for energy (as well as for Capital) implies that a change in energy will cause a 30% as large change in GDP. But energy data from the OECD[6] and Gross World Product data from the World Bank[7] imply that the actual relationship between change in Energy and change in GWP is closer to 1 to 1—see Figure 41 and Figure 42.
Figure 41: Regressing change in GDP against change in Energy
This data is very hard to reconcile with the Cobb-Douglas production function. Ironically, Neoclassical economists unintentionally pointed out that this data in fact contradicts the Neoclassical theory of income distribution—which is that “factors of production” (Labour, Capital, And Energy) are paid their marginal products.
if the elasticity of substitution s between brown energy and other inputs is literally zero (Leontief) then production falls one-for-one with energy supply… The strict Leontief case makes nonsensical predictions with regard to the evolution of marginal products, prices and expenditure shares… If factors markets are competitive so that factor prices equal marginal products, this then implies that similarly the price of energy jumps to 1/a [the exponent for energy] and the prices of other factors fall to zero… We consider these predictions to be economically nonsensical. {Bachmann, 2022 #6606, p. 11}
Those predictions are indeed nonsensical, but at the same time, the empirical data does show a 1:1 relationship between change in energy and change in GDP: see Figure 41 and Figure 42. Therefore, the assumptions that Neoclassical economists make—that “factor prices equal marginal products”—must be false. This is confirmed in the Appendix to this chapter.
The reason, also inadvertently given by these Neoclassical economics when they say consider, and then reject, the possibility that “the elasticity of substitution s between brown energy and other inputs is literally zero”, is that there is no substitute for energy. In general, you cannot substitute any other input for energy: if you don’t have energy at all for your car, you can’t put Labour or Capital in the tank instead. Also, capital machinery is designed for a specific form of energy: if you don’t have any petrol for your ICE car, you can’t put electricity in its place. The elasticity of substitution between energy and other factors of production is literally zero, while the substitutability of one form of energy for another is also extremely low: to convert from one form of energy (“brown” or fossil fuels”) to another requires investment in new capital equipment designed for the new form of energy.
Conversely, the Leontief Production Function, which these Neoclassicals deride, fits this data extremely well. Applying the transformation in Equation to the Leontief Production Function provides an explanation for the statistical regularity that Leontief discovered.
Figure 42: Global Energy Consumption and Gross World Product
Dimensional analysis shows that the dimension of the product is Energy/Year:
GDP as conventionally used in scalar macroeconomic models, however, is dimensioned in terms of the number of universal commodities—“Widgets”—produced per year:
Using Q for the output of Equation , we have
If we now treat EK as the energy contained in a Widget, we get Equation :
We can now deduce that the “Capital to Output Ratio”, which was first identified as an empirical regularity by Leontief, without any explanation as to why it applied, is in fact the inverse of the efficiency with which machinery turns energy into useful work:
The Leontief Production Function is therefore fully compatible with an energy-based interpretation of how output is produced. It also shows that, to a first approximation, GDP is energy turned into useful work. The models shown in Chapter 7, which used a Leontief Production Function, can therefore be updated to be fully consistent with the role of energy in production by replacing the Capital to Output Ratio with its inverse, the efficiency of conversion of energy into useful work.
Appendix: The Faulty Statistics of Cobb and Douglas
The exponents in the Cobb-Douglas Production Function were allegedly derived empirically from index number data collated by the economist Paul Douglas. I said “allegedly” because Cobb and Douglas’s core empirical result was erroneously derived.
Cobb and Douglas fitted a function without the “Total Factor Productivity” (TFP) term, and they reported exponents for L and K of 0.75 and 0.25 respectively:
The fact that these alleged empirical results were consistent with the Neoclassical theory of income distribution played a very large role in the acceptance of the CDPF by Neoclassical economists. Robert Solow, who was given the “Nobel” Prize in Economics for his work on growth theory, once remarked that:
“had Douglas found labor's share to be 25 per cent and capital's 75 per cent instead of the other way around, we would not now be discussing aggregate production functions” {Fisher, 1971 #6378`, p. 305}.
They did two correlation calculations, one with the raw index data—columns 2 to 4 in Table 9 and Table 10—and one with what they described as the data “with trends eliminated”. An extremely high correlation for the raw data is to be expected for data trending in the same direction, and they reported a coefficient of 0.97. However, they also reported a very high correlation coefficient of 0.94 for the data “with trends eliminated”:
The coefficient of correlation between P and P' with trends included is .97 and with trends eliminated is .94. {Cobb, 1928 #4910`, p. 154}
These very high correlations played a significant role in the ultimate acceptance of their production function, but the manner in which they derived their “with trends eliminated” data was spurious. It appears that they performed a correlation of the differences between the index data for GDP and its 3-Year moving average, and the differences between the functional data for GDP and its 3-Year moving average, using the value derived from the regression “with trends included”:
Moreover the fact that the deviations of P' and P from their respective three year moving averages move closely together as is shown by Chart III and that they have a correlation coefficient of +.94 indicates that the relationship is not merely one between factors whose secular trend happens to be upward. {Cobb, 1928 #4910, p. 160}
However, this result is spurious, because the sign of the deviation of both series from their moving averages are normally the same—see the last two columns in Table 9. This is why their correlation for the data “with trends eliminated” was so high.
The modern method to eliminate trends from data is to take log differences, as shown in Table 10. The alpha coefficient derived from this data is minus 0.11. Had Cobb and Douglas performed this calculation themselves, it is likely that their paper would never have been submitted to a journal, let alone published.
More recent data (see Table 11) does not redeem the CDPF. Regressing the function on the log difference data returns (with an R2 of 0.45), which is also inconsistent with the Neoclassical theory of income distribution.
Neoclassical economists were spared this unfortunate discovery by Robert Solow, who introduced the A term for “Total Factor Productivity” in his 1957 paper “Technical change and the aggregate production function” {Solow, 1957 #5296}. Solow’s motivation was the desire to distinguish “variations in output per head due to technical change from those due to changes in the availability of capital per head” {Solow, 1957 #5296, p. 312}. However, since no time series exists for “Total Factor Productivity”, its value had to be imputed from the data for GDP, Labor and Capital with the assumption that the exponents derived by Cobb and Douglas were correct. Solow put it this way:
Naturally, every additional bit of information has its price. In this case the price consists of one new required time series, the share of labor or property in total income, and one new assumption, that factors are paid their marginal products. Since the former is probably more respectable than the other data I shall use, and since the latter is an assumption often made, the price may not be unreasonably high. {Solow, 1957 #5296, p. 312}
This led to the rate of change of TFP being calculated as a residual from the rates of change of GDP, Labor and Capital, given an assumed value for the a coefficient. The rate of change of TFP has become known as “the Solow Residual”, and accounts for about 85% of measured economic growth. As shown above, this is because Solow’s Residual inadvertently measured, not some disembodied entity called “Total Factor Productivity”, but the contribution to output made by the energy inputs to a representative machine.
In conclusion, the Leontief Production Function is the only one that is consistent with the data on energy and GDP. The Cobb-Douglas Production Function, like so much else of Neoclassical economics, should be consigned to the dustbin of the history of economic thought.
[1] If you need to see the assumptions and definitions in this theory, check the Wikipedia entry: https://en.wikipedia.org/wiki/Marginal_revenue_productivity_theory_of_wages.
[2] It is often used in what is known as the “Constant Elasticity of Substitution” form. See https://en.wikipedia.org/wiki/Constant_elasticity_of_substitution for the details. Input-Output models of production, using matrix mathematics, were used for “Computable General Equilibrium” models in the 50-70s. These still exist, but the dominant class of models today, known as “Dynamic Stochastic General Equilibrium” (DSGE) models, treat output as a scalar.
[3] The data on capital is also problematic, because there is no simple way to measure capital independently of the distribution of income—see Sraffa’s work and the “Cambridge Controversies” over the measure and nature of capital—and because some calculation methods, including those used by the Penn World Tables, assume that the Cobb-Douglas Production is valid.
[4] “The empirical value for b of 1.01 merely reflected the inexactness of the regression for the initial base year” {Samuelson, 1979 #5387, p. 928}
[5] See https://exergyeconomics.wordpress.com/exergy-economics-101/what-is-exergy/.
[6] https://data-explorer.oecd.org/vis?lc=en&df[ds]=DisseminateArchiveDMZ&df[id]=DF_DP_LIVE&df[ag]=OECD&av=true&pd=%2C2022&dq=WLD.PRYENRGSUPPLY...A&to[TIME_PERIOD]=false&vw=tl&lb=bt.